
Zadanie Mityng (mit)
Pomóż nam usprawnić bazę zadań!
Mityng
Limit pamięci: 64 MB
Burmistrz Bajtogrodu w celu poprawienia swych notowań, postanowił zorganizować mityng lekkoatletyczny. Niestety Bajtogród nie posiada stadionu, ani hali lekkoatletycznej, zatem wszelkie konkurencje będą odbywały się na ulicach miasta. Burmistrz postanowił ograniczyć się do konkurencji biegowych i poprosił Cię o wytyczenie tras.
Sieć drogowa Bajtogrodu składa się z  skrzyżowań i
skrzyżowań i 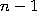 łączących je ulic. Z każdego
skrzyżowania można dojechać ulicami do dowolnego innego.
Trasa biegowa musi zaczynać się na pewnym skrzyżowaniu, przebiegać pewną liczbą ulic
i kończyć się na innym skrzyżowaniu.
Burmistrz chce, aby w jednocześnie
odbywało się jak najwięcej konkurencji, należy więc wyznaczyć jak największą liczbę tras.
Z powodów bezpieczeństwa, żadne dwie trasy nie mogą mieć wspólnych skrzyżowań lub ulic.
Co więcej, nie wszystkie skrzyżowania nadają się do tego, by umieścić na nich start lub metę.
łączących je ulic. Z każdego
skrzyżowania można dojechać ulicami do dowolnego innego.
Trasa biegowa musi zaczynać się na pewnym skrzyżowaniu, przebiegać pewną liczbą ulic
i kończyć się na innym skrzyżowaniu.
Burmistrz chce, aby w jednocześnie
odbywało się jak najwięcej konkurencji, należy więc wyznaczyć jak największą liczbę tras.
Z powodów bezpieczeństwa, żadne dwie trasy nie mogą mieć wspólnych skrzyżowań lub ulic.
Co więcej, nie wszystkie skrzyżowania nadają się do tego, by umieścić na nich start lub metę.
Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita  (
(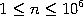 )
oznaczająca liczbę skrzyżowań w Bajtogrodzie.
Skrzyżowania są numerowane od 1 do
)
oznaczająca liczbę skrzyżowań w Bajtogrodzie.
Skrzyżowania są numerowane od 1 do  .
Kolejne
.
Kolejne 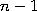 wierszy zawiera opisy ulic:
każdy opis składa się z dwóch liczb całkowitych
wierszy zawiera opisy ulic:
każdy opis składa się z dwóch liczb całkowitych 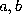 (
(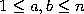 ,
,  )
oznaczających, że skrzyżowania o numerach
)
oznaczających, że skrzyżowania o numerach  i
i 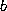 są połączone ulicą.
są połączone ulicą.
W kolejnym wierszu znajduje się liczba całkowita 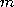 (
(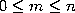 ) oznaczająca liczbę
skrzyżowań, na których można umieścić start lub metę. Ostatni wiersz wejścia zawiera
) oznaczająca liczbę
skrzyżowań, na których można umieścić start lub metę. Ostatni wiersz wejścia zawiera 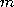 liczb
oznaczających numery tych skrzyżowań.
liczb
oznaczających numery tych skrzyżowań.
Wyjście
W jedynym wierszu wyjścia należy wypisać jedną liczbę całkowitą oznaczającą, ile maksymalnie można wyznaczyć tras biegowych.
Przykład
Dla danych wejściowych:
5 1 2 3 2 4 1 1 5 4 1 2 5 4
poprawną odpowiedzią jest:
1
Autor zadania: Tomasz Idziaszek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English